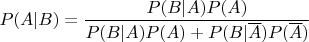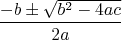Most of us are not
Donald Knuth, and indeed need to
test our software. That is even true for my hobby projects - when I offer software for use by others, it's a matter of craftmanship to deliver the best software possible. It's very hard to foresee all the possible environments (architecture, compiler, library version, ...) where my software might be run. But at least, I can minimize the number of programming errors by testing things as much as possible.
The trouble with testing, however, is that it is dead boring. I hate doing boring things -- life is just too short. So, I want to do my testing in the least boring way possible -- I'd like to be able to simply run:
$ make test
and have that go through all my test cases, and report any failures. The idea is that if it is so easy to run tests, you might actually do so, and make sure your software is working according to plan. When doing a release, it is so easy to forget something really obvious, for which you get embarrasing bug reports... Running some automated tests gives some peace of mind when doing a release.
gtest
Since 2.16, the
GLib library offers a unit-testing framework called
GTest (note, this is not to be confused with
Google Test, sometimes also called GTest). GTest is not much different from, say,
check, but it's part of GLib and integrates nicely with it. I have started to use it for mu, and I am quite happy with it. Here, I will not go into the details of actually
writing test cases, but talk about how to integrate GTest with your code. For the best results, you'd probably want to integrate it with your build system. I am using autotools.
The overall setup is that for all my directories with code, there is a subdirectory tests/ which contains the test code. Those test cases are unit-tests, which test one function or a couple of them combined. Now, of course it's a lot easier when your code is written in such a way that makes this easy[1]. In addition to the per-directery tests/, there is also a top-level tests/, which tests the whole software workflow. In the case of mu, this means that the tests will index some test messages, fill a database with that, and then run some test queries against this database. When all of that works correctly, I am quite confident that my software is not totally broken.
autotools
Now, let's discuss how you can integrate GTest with your code; this is inspired by the way GTK+ does it these days. First, here is
gtest.mk, a file in the top of my source tree, that I include in all
Makefile.ams that require GTest support:
TEST_PROGS=
test: all $(TEST_PROGS)
@ test -z "$(TEST_PROGS)" || gtester -l --verbose $(TEST_PROGS); \
test -z "$(SUBDIRS)" || \
for subdir in $(SUBDIRS); do \
test "$$subdir" = "." || \
(cd $$subdir && $(MAKE) $(AM_MAKEFLAGS) $@ ) || exit $? ; \
done
.PHONY: test
This blob adds a
test target to various
Makefiles, which will run the
gtester program (part of GTest) with your test programs.
In my
configure.ac I have:
# g_test was introduced in glib 2.16
PKG_CHECK_MODULES(g_test,glib-2.0 >= 2.16,
[have_gtest=yes],[have_gtest=no])
AM_CONDITIONAL(MU_HAVE_GTEST, test "x$have_gtest" = "xyes")
if test "x$have_gtest" = "xno"; then
AC_MSG_WARN([You need GLIB version >= 2.16 to build the unit tests])
fi
With this, I make sure that my code also works with older versions of GLib; the unit tests will only work with newer versions, of course. With this, you'll have a symbol
MU_HAVE_GTEST that you can use in your
Makefile.am; for example, in
index/Makefile.am, I have:
include $(top_srcdir)/gtest.mk
SUBDIRS= .
if MU_HAVE_GTEST
SUBDIRS += tests
endif
[....]
As you can see, it includes
gtest.mk mentioned above, and (conditionally) add
tests/ as a subdirectory to visit.The unit tests are in this subdirectory. Note that by explicitly setting
SUBDIRS to '.' first, we ensure that first we build the code in index, before we go to
tests/.
unit tests
Below is a simple example unit test program; it only uses a small subset of GTest. You can further organize your test cases (see
GTestSuite and
GTestCase) and see
Fixtures, which setup the testing environment. I don't use those, but they might be useful for others. In general, I am only using a small subset; check out the GTest-documentation to find out more. Anyway, here are some simple test cases:
#include <glib.h>
#include "my-code-to-test.h"
static void
test_num_str (void)
{
char *str;
g_assert_cmpstr (str = my_num_str(1001),==,"one thousand and one");
g_free (str);
g_assert_cmpstr (str = my_num_str(-1),==,"minus one");
g_free (str);
}
static void
test_warning (void)
{
/* no complex roots: my_sqrt(-1) should
* return MY_SQRT_ERROR and issue a g_warning; the
* g_warning will trigger the process to fail,
* which is what we're expecting */
if (g_test_trap_fork (0, G_TEST_TRAP_SILENCE_STDERR))
g_assert (my_sqrt (-1) == MY_SQRT_ERROR);
g_test_trap_assert_failed ();
}
int
main (int argc, char *argv[])
{
g_test_init (&argc, &argv, NULL);
g_test_add_func ("/mytests/test-add", test_add);
g_test_add_func ("/mytests/test-warning", test_warning);
return g_test_run ();
}
Now, we can run our tests with:
$ make test
(Note that the test cases are
fork()ed, and you can actually write a test case where it
passes if an
abort or even a segfault occurs.)
For mu-0.4 I get the following output:
[...]
make[1]: Entering directory `/home/djcb/src/mu-0.4/tests'
TEST: test-index-search... (pid=15553)
/all/test-query01: OK
/all/test-query02: OK
/all/test-query03: OK
/all/test-query04: OK
/all/test-query05: OK
/all/test-query06: OK
/all/test-query07: OK
/all/test-stats01: OK
PASS: test-index-search
make[1]: Leaving directory `/home/djcb/src/mu-0.4/tests'
Nice and easy; if you're less lucky, you might get something like:
make[1]: Entering directory `/home/djcb/src/mu-0.4/tests'
TEST: test-index-search... (pid=16024)
/all/test-query01: **
ERROR:test-index-search.c:117:query_01: assertion failed (mu_msg_sqlite_get_subject(row) == "this can't be right"): ("Re: What does 'run' do in cperl-mode?" == "this can't be right")
FAIL
GTester: last random seed: R02S2d24e3907b0c62e6a008e891f401fedf
/bin/bash: line 5: 16023 Terminated gtester --verbose test-index-search
make[1]: Leaving directory `/home/djcb/src/mu-0.4/tests'
With that, all we need to do is fix the bug and test again... rinse-lather-repeat. Using GTest, it's really easy to run test cases. In general I try to keep my software pass the tests at the end of every programming session. Now, this does not work when I do
big changes, but after stabilizing things again, I make sure all test cases pass, both old and new.
parting thoughts
One thing still missing from GTest is some way to see the
code coverage, i.e. to see which part of the code are covered by tests. I think it should be possible to do this using
gcov, but it'd be nice if someone automated that a bit. Another issue is that for effective use, you will need something like the setup described here. One can hardly expect someone new to Unix-development to figure this out by themselves... but of course, we cannot really blame GTest for that.
Hopefully my setup helps a bit to setup non-boring testing (even though it might be a bit boring in itself...). There are real-life examples of this in both mu and GTK+. And finally, if you find any inaccuracies, please let me know -- there are no unit tests for blog entries to save me from mistakes...
[1] Now, a discussion of how to write easily testable functions deserves its own blog entry, but there are some general things to keep in mind. Keep your functions short, limit the number of parameters, avoid global variables, limit side-effects to only a few functions, etc. In other words, use the lessons learnt from functional programming languages. And as a nice side-effect (ha!), such functions tend to be much less error-prone in the first place.

 :
: